Il pendolo e il tempo

Carroll descrive diverse volte contesti in cui mancano effetti gravitazionali. Uno di questi lo  si trova proprio in “Alice nel paese delle meraviglie”, quando Alice, inseguendo il Coniglio Bianco, si sporge su una buca dietro la siepe per cadere per un lunghissimo tempo. Anche in questo caso, dunque, si immagina una caduta libera.

Esiste una edizione di “Alice” annotata dal matematico Martin Gardner (1914 – 2010). In particolare, Gardner commenta proprio questo brano osservando che il problema della caduta libera attraverso un buco che attraversi il centro della terra era molto dibattuto tra i contemporanei di Carroll. Tuttavia, la soluzione corretta si ritrova già in Galileo (Dialogo dei Massimi sistemi, Giornata Seconda, ediz. di Firenze 1842, vol. 1, pagg 251-252) che avrebbe spiegato – attualizzandolo nei termini descritti nel romanzo per ragazzi – che Alice percorrerebbe un moto incessante ed oscillatorio (immaginando che si possano trascurare tutti gli attriti), accelerando fino al centro della terra per poi decelerare, fermarsi, invertire il moto ed accelerare di nuovo verso il centro della terra e così via all’infinito.

In Sylvie and Bruno Carroll fa descrivere ad un professore tedesco un metodo – che utilizza lo stesso principio sopra descritto – per fare andare i treni con la forza di gravità come unica fonte di energia. Le rotaie dovrebbero attraversare il pianeta lungo una galleria perfettamente dritta che unisca i due luoghi che devono essere collegati.

Potrebbe risultare difficile immaginare una siffatta galleria. Ad una prima, veloce lettura, infatti, non si coglie con immediatezza cosa l’autore intenda per dritto. Dobbiamo infatti distinguere il sistema geometrico opportuno all’interno del quale inquadrare il problema. Il tipo di geometria che conosciamo tutti, per averla studiata a scuola, è, ovviamente, quella euclidea.

Ma la superficie del nostro pianeta non è descrivibile secondo la geometria euclidea. Occorre – come è risaputo – un tipo di geometria detta non-euclidea.

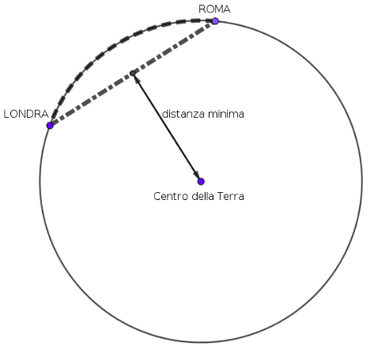
Si badi che il tipo di galleria che ipotizza Carroll non ha nulla a che vedere con quello che conosciamo sulla superficie della terra, perché, in quest’ultimo caso, la galleria - che noi percipiremmo come rettilinea - sarebbe invece un arco di circonferenza (nella figura la linea tratteggiata che unisce Londra e Roma). La Galleria di Carroll è invece davvero un segmento che attraversa una parte del pianeta per sbucare in un altro luogo sulla superficie (la linea tratto-punto che unisce le due città).